Solving Problems in the Panel Regression Model for Truncated
Dependent Variables: A Constrained Optimization Method
4.3 Empirical Findings About Boundary Violations
In terms of the boundary violations, none of the five models generate empirical violations,
due to the relatively stable statistics of democratic vote share. Unfortunately, in a two-party system, such as
in United States, this nice data property obscures the out-of-bound problem that is common in other contexts,
particularly within the scope of cross-national research that covers a very fragmented to one-party system.
However, considering theoretical boundary violations as Table 4 shows, the two panel
regressions without applying constrained optimization both suffer this problem at different levels. For the
original specification, there are 14 boundary violations, while Model II has 37 violations. With regard to
Model III, we cannot find an admissible solution in the original setting; therefore, we introduce a rescaled
parameter \eta that reduces the between-groups variability by multiplying a fraction as follows:
\begin{align*}
& {{p}^{*}_{1}}=a-\left( \bar{\bar{y}}+t_{{{\sigma }_{b}}}^{\min }\cdot {{\sigma }_{b}}\cdot \eta \right)\\
& {{q}^{*}_{1}}=b-\left( \bar{\bar{y}}+t_{{{\sigma }_{b}}}^{\max }\cdot {{\sigma }_{b}}\cdot \eta \right),
\end{align*}
where {{p}^{*}_{1}} and {{q}^{*}_{1}} are new lower and upper bounds for the demeaned dependent variable \left({{y}_{it}}-{{{\bar{y}}}_{i}}\right) . We start from 100% and decrease by 1% each time, and finally reach an admissible solution at \eta=60%. In this way, we derive a solution without theoretical boundary violation, but on the condition that it only applies to those counties where the average democratic vote share ranges from 26.48% to 63.67%, which numbers 95.57% in all 1964 counties.
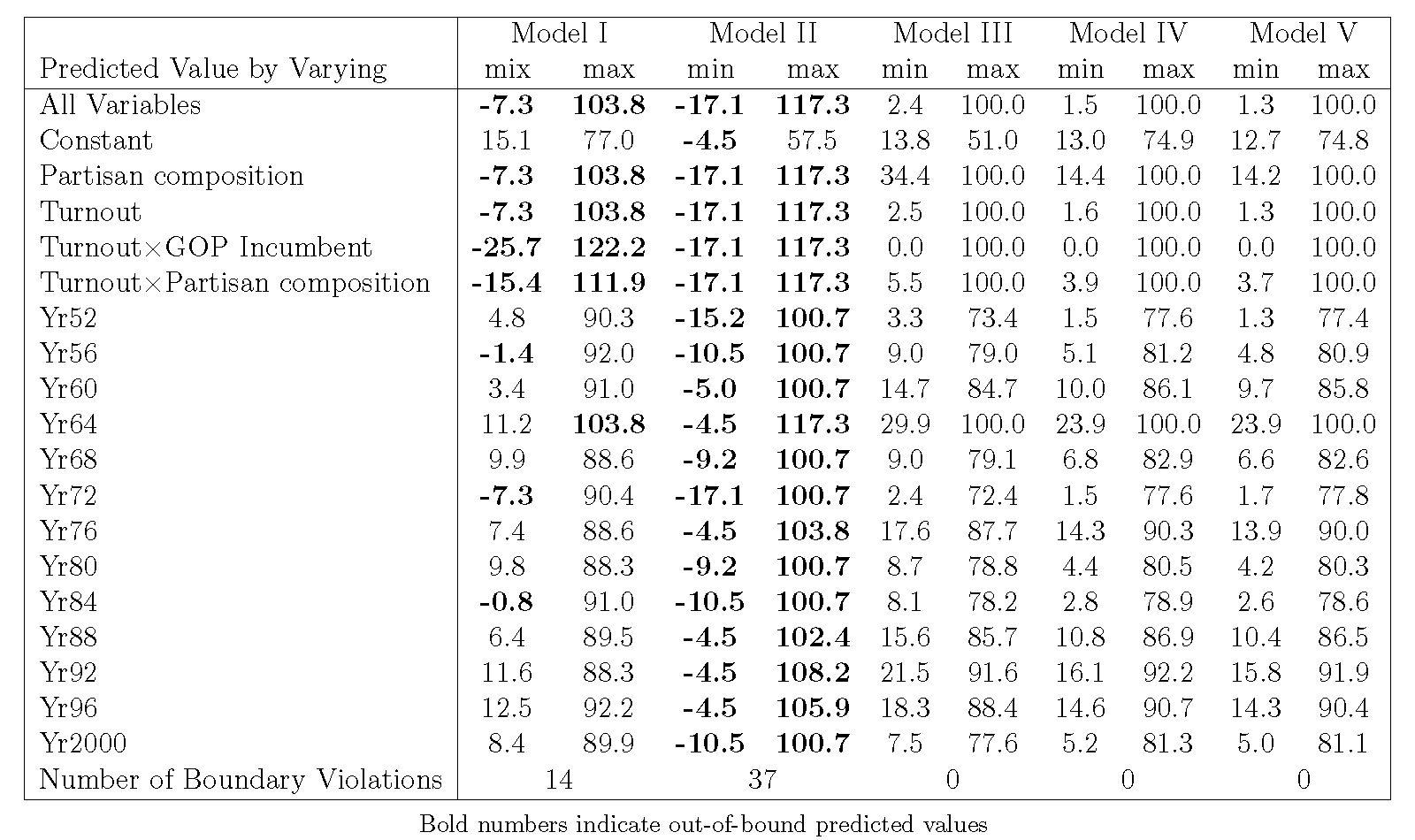
Table 4 Translation of Boundary Violations into Predicted Values For Model I to Model V
At last, the two models that use maximum likelihood estimation successfully eliminate theoretical boundary violations. Their estimates are relatively stable, regardless of whether the demeaning bias is corrected. Findings in both models are far more conservative than the original panel regression, and only one of the four explanatory variables (Partisan composition) has a significant relationship. Moreover, the standard error measures are also larger, and hence lead to smaller t values. These findings indicate that, the current panel regression tends to generate lenient results and likely to suffer from the problem of false significance.
